Question

EspanolooWhile making up his schedule for spring semester, Tom complains that he doesn't have very many choices of schedule because ofthe general education requirements he has to meet. His advisor tells Tom that he has to take one course from each of English (7choices), History (8 choices), Math/Stats (7 choices), Computer Science (6 choices), and general Science (8 choices). Does Tomhave a legitimate gripe?ED(a) If every possible course is available at the time he's registering, how many possibleschedules can he choose from (disregarding when the classes meet)?х5Tom can choose frompossible schedules.(b) In an unprecedented effort to make the general education requirements more accessible,the dean of Tom's college decides to double the number of acceptable courses in each ofthose five areas. What effect does this have on the number of possible schedules?CheckSave For LaterSubmit Assignment

Answer 1

The problem says Tom has to take one course from each of the following:

English (He has 7 different options for this)

History (8 different choices)

Math/Stat (7 different choices)

Computer Science (6 different choices)

General Science (8 choices)

In order to find the number of possible schedules he can choose, we can use the Fundamental Counting Principle, which states that if there are x ways to do one thing and y ways to do another thing, then there are x*y ways to do both.

Then, we know the number of choices or options for each course, then the possible schedules that Tom can choose are:

`\begin{gathered} S=E\cdot H\cdot M\cdot C\cdot S \\ S=7\cdot8\cdot7\cdot6\cdot8 \\ S=18816 \end{gathered}`

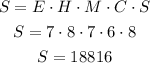
Tom can choose from 18816 possible schedules.

b) The dean of Tom's college decides to double the number of acceptable courses in each of those five areas, which means the new choices for each one is:

English (He has 7*2=14 different options for this)

History (8*2=16 different choices)

Math/Stat (7*2=14 different choices)

Computer Science (6*2=12 different choices)

General Science (8*2=16 choices).

Then, the new possible schedules are:

`\begin{gathered} S=14\cdot16\cdot14\cdot12\cdot16 \\ S=602112 \end{gathered}`

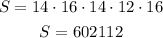
Then, the effect of this decision is the number of possible schedules is much greater than the first one, there are more possibilities.

The number of possible schedules increased by a factor of 2^5=32