Question

Suppose 24.9 g of nickel (II) bromide is dissolved in 300. mL of a 0.60 M aqueous solution of potassium carbonate.Calculate the final molarity of nickel(II) cation in the solution. You can assume the volume of the solution doesn't changewhen the nickel(II) bromide is dissolved in it.Round your answer to 3 significant digits.M0X3?EDoloArBHhx:CA

Answer 1

Step-by-step explanation

Given that:

Mass of nickel (II) bromide (NiBr₂) that dissolved = 24.9 g

The volume of the aqueous solution of potassium carbonate (K₂CO₃) = 300 mL = 0.300 L

The molarity of K₂CO₃ = 0.60 M

What to find:

The final molarity of nickel(II) cation in the solution.

Step-by-step solution:

The first step is to write the balanced chemical equation for the reaction.

NiBr₂ + K₂CO₃ → NiCO₃ + 2KBr

The next step is to calculate the moles of NiBr₂ using:

`\begin{gathered} Moles\text{ }(n)=\frac{mass\text{ }(m)}{M\text{ }(Molar\text{ }mass)} \\ \\ Molar\text{ }mass\text{ }of\text{ }NiBr₂=218.53\text{ }g\text{ /}mol \\ \\ Moles\text{ }of\text{ }NiBr₂=\frac{24.9g}{218.53g\text{/}mol}=0.1139\text{ }mol \end{gathered}`

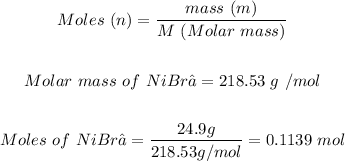
Also, the moles of K₂CO₃ can be calculated using:

`\begin{gathered} Moles=Molarity* Volume\text{ }in\text{ }L \\ \\ Moles\text{ }of\text{ }K₂CO₃=0.60M*0.300L=0.1800\text{ }mol \end{gathered}`

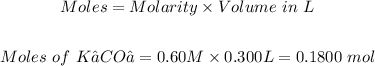
Using the mole ratio of NiBr₂ to K₂CO₃ from the equation above, that is (1:1)

we can say that K₂CO₃ is in excess.

So 0.1139 mol NiBr₂ gets converted into NiCO₃.

Hence, the final molarity of nickel(II) cation in the solution can be calculated using:

`Molarity=\frac{Moles\text{ }of\text{ }Ni\text{ }in\text{ }solution}{Volume\text{ }of\text{ }solution}=(0.1139mol)/(0.300L)=0.380\text{ }M`

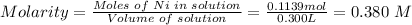
Hence, the of nickel(II) cation in the solution is 0.380