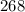Question

Admission to a baseball game is $3.50 for general admission and $6.00 for reserved seats. The receipts were $4233.00 for1018 paid admissions. How many of each ticket were sold? (Round to nearest integer if necessary.)Answer

Answer 1

Given that:

- Admission is $3.50 for general admission.

- Admission is $6.00 for reserved seats.

- The receipts were $4233.00.

- The total number of paid admissions was 1018.

Let be "g" the number of general admission tickets and "r" the number of reserved seat tickets.

Using the data given in the exercise, you can write the following System of Equations:

`\begin{cases}3.5g+6r={4233} \\ g+r=1018{}\end{cases}`

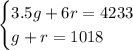
Where the first equation represents the total receipts (in dollars), and the second equation represents the total number of paid admissions.

You can solve the System of Equations using the Elimination Method:

1. Multiply the second equation by -6.

2. Add the equations.

Then:

`\begin{gathered} \begin{cases}3.5g+6r={4233} \\ -6g-6r={-6108}\end{cases} \\ ----------- \\ -2.5g=-1875 \\ \end{gathered}`

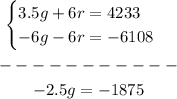
3. Solve for "g":

`\begin{gathered} g=(-1875)/(-2.5) \\ \\ g=750 \end{gathered}`

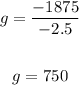
4. Substitute the value of "g" into the second original equation and solve for "r":

`\begin{gathered} \lparen750)+r=1018 \\ \\ r=1018-750 \\ \\ r=268 \end{gathered}`

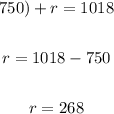
Hence, the answer is:

- Number of general admission tickets sold:

`750`

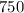
- Number of reserved seats tickets sold:

`268`