1 Answer

Mizzle · Answer 1 · 2023-05-26T22:44:45+0000

ANSWER

0.02 m³

Step-by-step explanation

By the Archimedes' Principle, the weight of a floating object is equal to the weight of the water displaced by the object,

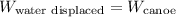
$W_{\text{water displaced}}=W_{\text{canoe}}$

This is,

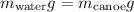
$m_{\text{water}}g=m_{\text{canoe}}g$

We know that the weight of the canoe is 200N, so there is no need to find its mass. Also, the mass is the product of the density and the volume,

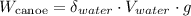
$W_{\text{canoe}}=\delta_(water)\cdot V_(water)\cdot g$

The density of water is 1000 kg/m³, the acceleration due to gravity g is 9.8m/s² and the weight of the canoe is 200N. Solve for the volume of water,

$V_(water)=(W_(canoe))/(\delta_(water)\cdot g)=\frac{200N}{1000\operatorname{kg}/m^3\cdot9.8m/s^2}=0.02m^3$

Hence, the volume of water displaced by the canoe is 0.02m³.

Please log in or register to add a comment.