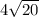Given:
Three of the vertices of a parallelogram are given as
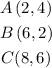
Required:
(a) Plot the point A, B and C in the coordinate plane
(b) Find the mid-point of diagonal AC
(c) Find the fourth vertex D
(d) Find the length of diagonal AC
(e) Find the perimeter of ABCD.
Step-by-step explanation:
Take D coordinate as (x,y)
now midpoint of AC and BD is same so
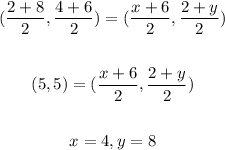
midpoint of AC
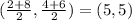
length of diagonal AC
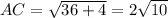
perimeter of ABCD
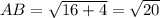
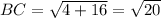
perimeter is
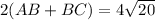
Final answer:
(b) Find the mid-point of diagonal AC
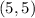
(c) Find the fourth vertex D
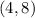
(d) Find the length of diagonal AC
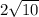
(e) Find the perimeter of ABCD.