ANSWER
0.306 or 30.6%
Step-by-step explanation
Note: Probability is the number of desired results divided by the total number of results.
Combination formula to apply:
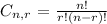
Desired Results:
3 brown worms from 7
4 red worms from 6
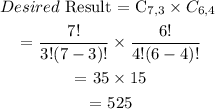
Total Result:
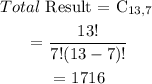
Determine the Probability
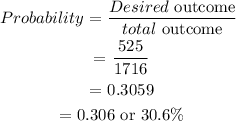
Hence, the probability that she will choose 3 brown worms and 4 red worms is 0.306 or 30.6%.