We need to find the sum of the interior angles of a convex nonagon.
First, let's remember that a nonagon is a polygon with 9 sides.
Also, the formula to find the sum of the interior angles for a convex polygon of n sides is:
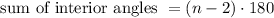
So, in this case, we have n = 9. Using this value in the above formula, we obtain:
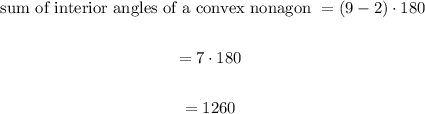
Therefore, the answer is 1260º.