If the scale factor of one figure to another one is k, then the ratio of their volumes is equal to:
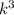
The volume in cubic inches of the smaller pyramid is 27, while the volume of the bigger pyramid is 343. Then:

Take the cubic root to both members of the equation to isolate k:
![\begin{gathered} \Rightarrow k=\sqrt[3]{(27)/(343)} \\ =\frac{\sqrt[3]{27}}{\sqrt[3]{343}} \\ =(3)/(7) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w90iei8ei6zi3kilyfee601f8gv029qr53.png)
Therefore, the scale factor of the smaller pyramid to the larger pyramid, is:
