Question

Elida will use six different wires for a science project. The fractions represent the diameters of these wires in inches. Least to greatest

Answer 1

If we are to arrange them from least to greatest,

First, let's covert to equaivalent fraction

`(7)/(16)=(7*2)/(16*2)=(14)/(32)`
`(1)/(2)=(1*16)/(2*16)=(16)/(32)`
`(3)/(8)=(3*4)/(8*4)=(12)/(32)`
`(9)/(32)`
`(5)/(16)=(5*2)/(16*2)=(10)/(32)`
`(15)/(32)`

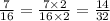
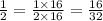
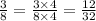
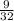
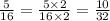
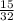
When we have fractions with the same denominator, the one with the smallest/least numerator is the smallest/least

So comparing the above, we can now arrange;

9/32 , 5/16 , 3/8 , 7/16 , 15/32 , 1/2