Question

How much should a family deposit at the end of every 6 months in order to have $4000 at the end of 3 years? The account pays 5.9% interest compounded semiannually[Round your final answer to two decimal places

Answer 1

We are asked to determine the present value of an annuity that is paid at the end of each period. Therefore, we need to use the formula for present value ordinary, which is:

`PV_(ord)=C((1-(1+i)^(-kn))/((i)/(k)))`

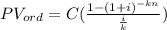
Where:

`\begin{gathered} C=\text{ payments each period} \\ i=\text{ interest rate} \\ n=\text{ number of periods} \\ k=\text{ number of times the interest is compounded} \end{gathered}`

Since the interest is compounded semi-annually this means that it is compounded 2 times a year, therefore, k = 2. Now we need to convert the interest rate into decimal form. To do that we will divide the interest rate by 100:

`(5.9)/(100)=0.059`

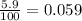
Now we substitute the values:

`PV_(ord)=4000((1-(1+0.059)^(-2(3)))/((0.059)/(2)))`

Now we solve the operations, we get:

`PV_{\text{ord}}=39462.50`

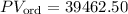
Therefore, the present value must be $39462.50