Question

How much of a radioactive kind of iodine will be left after 52 hours if the half-life is 13 hours and you start with 592,032 grams?

Answer 1

The formula for half-life is:

`A=A_0e^(kt)`

where A is the amount of the substance after a certain time

A₀ = the initial value of the substance

e = the natural number with a value of 2.71828

k = decay rate

t = time

These are the given information in the question.

At t = 13 hrs, A₀ = 592, 032 grams, A = half of 592, 032 grams = 296, 016 grams.

At 52 hrs, A₀ = 592, 032 grams, A = ?

Before we can solve for the final value of the substance after 52 hrs, we need to solve for the decay rate "k" first. To solve that, let's use the information given at 13 hrs.

`\begin{gathered} A=A_oe^(kt) \\ 296,016=592,032e^(k(13)) \end{gathered}`

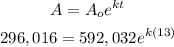
Solve for k. To do that, start dividing both sides by 592, 032.

`\begin{gathered} (296,016)/(592,032)=(592,032e^(13k))/(592,032) \\ (1)/(2)=e^(13k) \\ \ln (1)/(2)=13k \\ \text{Divide both sides by 13.} \\ k=(\ln (1)/(2))/(13) \\ k=-0.053319 \end{gathered}`

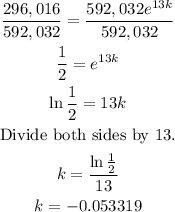
Therefore, the decay rate of iodine is 0.053319 or -5.3319%

Now, let's apply this decay rate to solve for the final value of the substance after 52 hrs.

`\begin{gathered} A=A_oe^(kt) \\ A=592,032e^(-0.053319(52)) \end{gathered}`

Solve for A.

`\begin{gathered} A=592,032e^(-2.772588) \\ A=592,032(0.0625) \\ A\approx37,002.03 \end{gathered}`

Hence, after 52 hours, there is an approximate of 37, 002.03 grams of iodine left.