(1) T, U and V are collinear which means they all lie on the same line segment.
Suppose U is between T and V and that TU = 7x - 4, and UV = 6x + 10 and TV = 45, find TU.
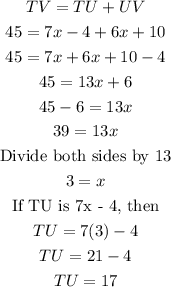
(2) Angles LMN + NMO + OMP = 180 (Angles on a straight line equals 180

(3) If on the line segment, Ef is 3x and FG is three times as long as EF, then FG is 3x times 3 which is 9x. Hence, you now have;
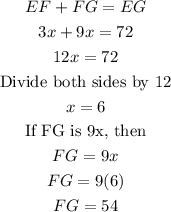
(4) If WZ = 32, and YZ = 6, that means WY is derived as

(5) Angles A and B are complementary, which means they both add up to 90 degrees. Therefore;
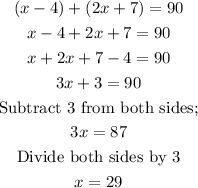
(6) Angle XWY = 83, and angle YWZ = 34. Angle XWZ is a combination of XWY and YWZ, therefore;
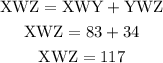
(7) If Line segment QS = 23, and QR = 7, then;
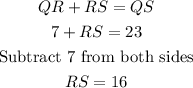
(8) If angle RSU = 76, observe that angles RST plus TSU equals angle RSU.
Therefore;

(9) If line segment JL measures 10x + 7, and line segment JK and KL added together equals line segment JL, then;

(10) Angles on a straight line equals 180, that means angle ABC plus angle CBD equals 180.
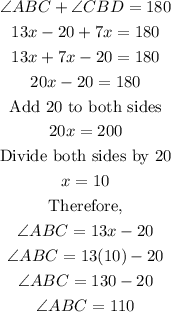
(11)