GIVEN:
We are given the equation of a line as follows;
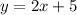
Required;
To find the equation of a line that is parallel to this line and that contains the coordinates;
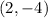
Step-by-step solution;
First thing to note is that, the equation of the line is given in the slope-intercept form. The slope-intercept form of a linear equation is generally written as;
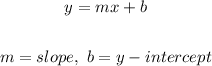
For a line that is parallel to another, the slopes are equal in value. This simply means the slope of the other line (the line parallel to the one given) is 2.
Note that the slope of the line given is;
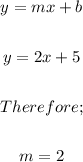
For a line that contains the point (2, -4) and the slope is 2, we can now write the following;
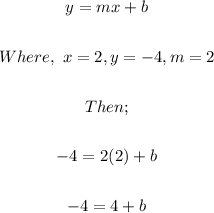
Now we subtract 4 from both sides of the equation;
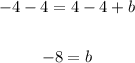
Now we have the slope and the y-intercept as;
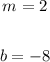
We can now write the equation of the line as follows;

Therefore.
ANSWER:
