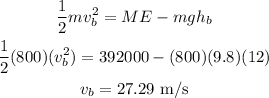Given data
*The given mass is m = 800 kg
*The given height is h = 50 m
*The speed at point A is v_A = 20 m/s
*The height at point B is h_b = 12 m
(a)
The formula for the mechanical energy is given as
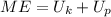
*Here U_k = 0 J is the kinetic energy
*Here U_p = mgh is the potential energy
Substitute the known values in the above expression as
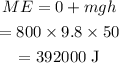
Hence, the mechanical energy is ME = 392000 J
(b)
The formula for the height at point A is given by the relation as
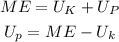
Substitute the known values in the above expression as
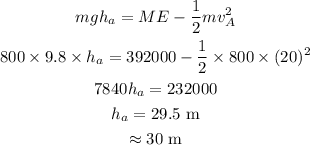
Hence, the height at point A is h_a = 30 m
(c)
The velocity at point B is calculated by the relation as
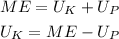
Substitute the known values in the above expression as