Question

Assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1 find the probability of a bone density test score between -1.79 and 1.79

Answer 1

To answer this question, first we need to convert our desired values(-1.79 and 1.79) to z-scores. The z-score formula is given by:

`z=(x-\mu)/(\sigma)`

Where mu represents the mean and sigma represents the standard deviation. Since the mean is 0 and the standard deviation is 1, our desired values are already z-scores. We can now just go to a z-table and check how much area of the graph we have between zero and 1.79, and then multiply by 2(since the normal distribution is symmetric, the distance between -1.79 and 0 is the same as the distance between 0 and 1.79).

Using a z-table

Now, we just multiply it by 2.

`0.4633*2=0.9266`

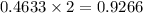
The probability of a bone density test score between -1.79 and 1.79 is 0.9266 or 92.66%.