So we're going to use the remainder theorem.
Remember that the remainder theorem is stated as follows: When a polynomial p(x) is divided by a linear polynomial b(x) whose zero is x = k, the remainder is given by r = p(k). This is, in our problem:
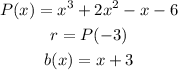
The first thing we're going to do is to divide:
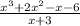
Using synthetic divition:
And, the value of P(-3) is -12.
So,
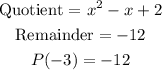
Using the theorem, notice that the remainder and P(-3) are the same.