Question

Exactly 3.3 s after a projectile is fired into the air from the ground, it is observed to have a velocity v⃗ = (8.6 i^ + 4.7 j^)m/s, where the x axis is horizontal and the y axis is positive upward. aDetermine the horizontal range of the projectile.bDetermine its maximum height above the ground.cDetermine the speed of motion just before the projectile strikes the ground.dDetermine the angle of motion just before the projectile strikes the ground.= ∘ below the horizontal

Answer 1

a. Horizontal range is given by,

`Range=(u^2sin2\theta)/(g)`

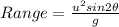
where u is the initial speed, and theta is the angle of projection,

Now velocity vector as a function of time is given by,

`\vec{v}(t)=(ucos\theta)\hat{i}+(usin\theta-gt)\hat{j}`

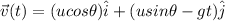
Given,

`\begin{gathered} \vec{v}(3.3s)=8.6\text{ }\hat{i}+4.7\text{ }\hat{j} \\ \Rightarrow ucos\theta=8.6,usin\theta-(10)(3.3)=4.7 \\ \Rightarrow ucos\theta=8.6,usin\theta=37.7 \\ Dividing, \\ \Rightarrow tan\theta=(37.7)/(8.6)=4.3837 \\ \Rightarrow\theta=77.15\degree \\ Hence \\ ucos77.15\degree=8.6 \\ \Rightarrow u=(8.6)/(0.2224)=38.67\text{ m/s} \end{gathered}`

And so, the horizontal range will be,

`Range=((38.67)^2sin(154.3\degree))/((10))=64.85\text{ m}`

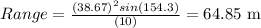
b. Maximum height reached by a projectile is given by,

`\begin{gathered} H_(max)=(u^2sin^2\theta)/(2g) \\ \Rightarrow H_(max)=((38.67)^2sin^2(77.15\degree))/((2)(10))=71.07\text{ m} \end{gathered}`

c. Now time of flight of the projectile is given by,

`t_(flight)=(2usin\theta)/(g)=((2)(38.67)sin(77.15\degree))/((10))=7.54\text{ s}`

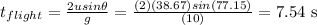
this is the time at which the projectile strikes the ground, and so its velocity then would be,

`\begin{gathered} \vec{v}(7.54s)=8.6\text{ }\hat{i}+(37.7-10*7.54)\hat{j} \\ \Rightarrow\vec{v}(7.54s)=8.6\text{ }\hat{i}-37.7\text{ }\hat{j} \end{gathered}`

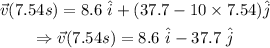
As expected the vertical component of velocity has just been flipped, and therefore its speed will be same as its initial speed i.e.

`v_{strikes\text{ }ground}=u=38.67\text{ m/s}`

d. Below the horizontal, let the angle be φ, then

`tan\varphi=-(v_y)/(v_x)`

extra -ve sign since its below the horizontal, when the projectile strikes the ground,

`\begin{gathered} v_y=-37.7\text{ m/s} \\ v_x=8.6\text{ m/s} \\ \Rightarrow tan\varphi=-((-37.7))/(8.6)=(37.7)/(8.6)=tan\theta \\ \Rightarrow\varphi=\theta \\ \Rightarrow\varphi=77.15\degree \end{gathered}`

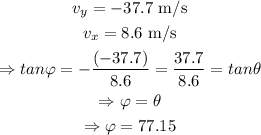
Result: a. 64.85 m, b. 71.05 m, c. 38.67 m/s, d. 77.15°.