When you have a polynomial with no independent term you can start by factorizing the polynomial, as follows:
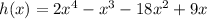
The common factor is x, then:

Now you have a third-degree polynomial inside the ( ), let's called it j(x):
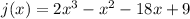
You need to factorize this polynomial, then find all the numbers that divide the independent term 9.
These numbers are:
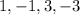
Let's probe if any of these numbers makes j(x)=0:
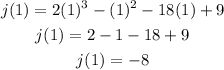
Then 1 is not a root, let's try -1:

Then -1 is not a root, let's try 3:
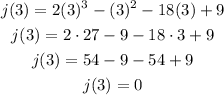
Then 3 is a root and you can apply synthetic division to find the others:
The new polynomial is:

Now you can factorize it as follows:
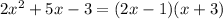
And finally, your 4th-grade polynomial can be written as:
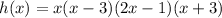
Thus, the zeros are at:
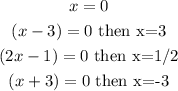
The answer is 0, 3, 1/2 and -3