Question

The profit for a certain commodity, n, where n is in units, is given by the functionP(n) =25n^2 + 300n + 1125At the break-even point, the profit is zero, i.e., P(n) = 0. Find the number of units where the break-even point is located, i.e., find n when P(n) = 0.The number of units, n, where the break-even point is located, isHint: Did you factor the GCF? Then reduce your equation to smaller coefficients?

Answer 1

Given the function:

`P\mleft(n\mright)=-25n^2+300n+1125`

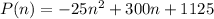
You know that "P" is the profit for a certain "n" commodity (in units).

You need to find the value of "n" when:

`P(n)=0`

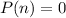
In order to find it, you can follow these steps:

1. Substitute this value into the function:

`P(n)=0`

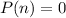
Then:

`\begin{gathered} 0=-25n^2+300n+1125 \\ \\ -25n^2+300n+1125=0 \end{gathered}`

2. Divide both sides of the equation by -25:

`\begin{gathered} (-25n^2)/((-25))+(300n)/((-25))+(1125)/((-25))=(0)/((-25)) \\ \\ n^2-12n-45=0 \end{gathered}`

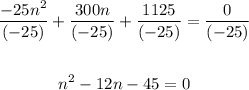
3. Factor the equation by finding two numbers whose Sum is -12 and whose Product is -45. These are 3 and -15, because:

`\begin{gathered} 3-15=-12 \\ \\ (3)(-15)=-45 \end{gathered}`

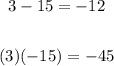
Then:

`(n+3)(n-15)=0`

4. Set up these two equations:

`\begin{gathered} n+3=0\text{ (Equation 1)} \\ \\ n-15=0\text{ (Equation 2)} \end{gathered}`

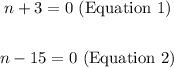
5. Solving form "n" from each equation, you get:

`\begin{gathered} n+3=0\text{ }\Rightarrow n_1=-3 \\ \\ n-15=0\Rightarrow n_2=15 \end{gathered}`

Since the number of units cannot be negative, the answer is:

`n=15`