Given the monthly payments for each one of the two terms, we can calculate the total repayment of the 5-year and 10- years term.
As for the 5-year plan,
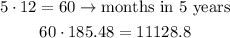
Similarly, for the 10-year plan,
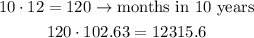
Finally, the difference between these two quantities is

The answer is 'The 5-year term would be 1186.80 lower', option B