Question

. (15 points) You work at a canning factory that's producing cans for a new brand of soup. You needto decide what size the cans should be. The soup cans can have a radius of either 2 in, 2.5 in, 3 in, or3.5 in. The cans need to hold a volume of exactly 90 in. The company wants the cans to be no morethan 5 inches tall, and it wants the cans to have the greatest lateral surface area possible so it canprint more information on the side of the cans.To solve this problem, you will fill in this table with the surface area and volume of each cylinder:

Answer 1

A can is shaped like a cylinder. The formula to find the volume of a cylinder is

`\begin{gathered} V=\pi r^2h \\ \text{ Where} \\ \text{ V is the Volume} \\ r\text{ is the radius and} \\ h\text{ is the height of the cylinder} \end{gathered}`

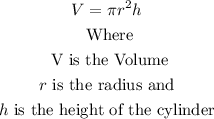
Now, you calculate the height that each can should be, given the radius and the volume. For this you can clear at once, the height of the formula shown:

`\begin{gathered} V=\pi r^2h \\ \text{ Divide by }\pi r^2\text{ from both sides of the equation} \\ \frac{V}{\text{ }\pi r^2}=\frac{\pi r^2h}{\text{ }\pi r^2} \\ \frac{V}{\text{ }\pi r^2}=h \end{gathered}`

Then, you have

*Radius = 2in

`\begin{gathered} \frac{V}{\text{ }\pi r^2}=h \\ \frac{90in^3}{\text{ }\pi(2in)^2}=h \\ \frac{90in^3}{\text{ }\pi\cdot4in^2}=h \\ (90in^3)/(4\pi in^2)=h \\ \frac{90}{4\pi^{}}in=h \\ 7.2^{}in=h \end{gathered}`

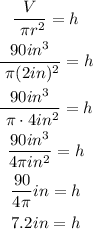
*Radius = 2.5 in

`\begin{gathered} \frac{V}{\text{ }\pi r^2}=h \\ \frac{90in^3}{\text{ }\pi(2.5in)^2}=h \\ \frac{90in^3}{\text{ }\pi\cdot6.25in^2}=h \\ (90in^3)/(6.25\pi in^2)=h \\ \frac{90^{}}{6.25\pi}in=h \\ 4.6in=h \end{gathered}`

*Radius = 3 in

`\begin{gathered} \frac{V}{\text{ }\pi r^2}=h \\ \frac{90in^3}{\text{ }\pi(3in)^2}=h \\ \frac{90in^3}{\text{ }\pi9in^2}=h \\ (90in^3)/(9\pi in^2)=h \\ (90)/(9\pi)in=h \\ 3.2in=h \end{gathered}`

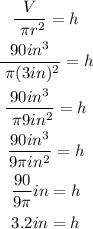
*Radius = 3.5 in

`\begin{gathered} \frac{V}{\text{ }\pi r^2}=h \\ \frac{90in^3}{\text{ }\pi(3.5in)^2}=h \\ \frac{90in^3}{\text{ }\pi12.25in^2}=h \\ \frac{90in^3}{\text{ }12.25\pi in^2}=h \\ \frac{90}{\text{ }12.25\pi}in=h \\ 2.3in=h \end{gathered}`

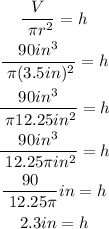
Then, the table filled out with the radii, heights, and volumes of the cans would be:

Now, you can calculate the lateral surface area of ​​each can using this formula:

`\begin{gathered} \text{ Lateral Surface Area }=2\pi rh \\ \text{ Where} \\ r\text{ is the radius and} \\ h\text{ is the height of the cylinder} \end{gathered}`

Then, you have

*2 in radius can:

`\begin{gathered} r=2in \\ h=7.2in \\ \text{ Lateral Surface Area }=2\pi rh \\ \text{ Lateral Surface Area }=2\pi(2in)(7.2in) \\ \text{ Lateral Surface Area }=2\pi\cdot14.4in^2 \\ \text{ Lateral Surface Area }=90.5in^2 \end{gathered}`

*2.5 in radius can:

`\begin{gathered} r=2.5in \\ h=4.6in \\ \text{ Lateral Surface Area }=2\pi rh \\ \text{ Lateral Surface Area }=2\pi(2.5in)(4.6in) \\ \text{ Lateral Surface Area }=2\pi\cdot11.5in^2 \\ \text{ Lateral Surface Area }=72.3in^2 \end{gathered}`

*3 in radius can:

`\begin{gathered} r=3in \\ h=3.2in \\ \text{ Lateral Surface Area }=2\pi rh \\ \text{ Lateral Surface Area }=2\pi(3in)(3.2in) \\ \text{ Lateral Surface Area }=2\pi\cdot9.6in^2 \\ \text{ Lateral Surface Area }=60.3in^2 \end{gathered}`

*3.5 in radius can:

`\begin{gathered} r=3.5in \\ h=2.3in \\ \text{ Lateral Surface Area }=2\pi rh \\ \text{ Lateral Surface Area }=2\pi(3.5in)(2.3in) \\ \text{ Lateral Surface Area }=2\pi\cdot8.1in^2 \\ \text{ Lateral Surface Area }=50.6in^2 \end{gathered}`

Then, the table filled out with the radii, heights, lateral surface areas, and volumes of the cans will be:

Therefore, the cans must have a radius of 2.5 inches and a height of 4.6 inches, since they will have a volume of 90 cubic inches, will not exceed 5 inches in height, and will have the maximum possible lateral surface.