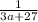Question

Multiply and/ or divide and put into lowest terms

Answer 1

`((3)/(a^2-81))/((9)/(a-9))`

the division of fractions follows the stes

`((a)/(b))/((c)/(d))=(a\cdot d)/(b\cdot c)`

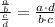
Applying this into the expression given

`(3\cdot(a-9))/(9\cdot(a^2-81))`

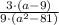
simplify the coefficients by decomposing 9 into a product and cancelling the common factors

`(3\cdot(a-9))/(3\cdot3\cdot(a^2-81))`

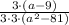
simplify

`(a-9)/(3\cdot(a^2-81))`

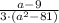
In the denominators there is a difference of squares that can be rewriten as a product, in which by definition the difference of square is described as

`a^2-b^2=(a+b)\cdot(a-b)`

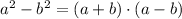
In the denominator of the expression we can see that a is squared and that 81 has an exact root which is 9, reason why we can write this as a difference of squares, it should look like this:

simplify the expression

`(1)/(3\cdot(a+9))`

distribute the 3

`(1)/(3a+27)`