Question

Write the numbers that will fill in the eighth row of Pascal’s triangle.

Answer 1

To answer this question, we're going to use some important properties of the Pascal's triangle.

1) If we number the rows starting at zero, then the kth row has k + 1 elements.

2) If we number the elements on the kth row starting with zero, then the mth element of row k is given by

`\begin{pmatrix}{k} \\ {m}\end{pmatrix}=(k!)/(m!(k-m)!)`

Using those two properties, we can answer our question.

We want to know the numbers that will fill in the eighth row, this means our k = 8.

From the first property, we know that we have 9 elements on this row, and they are given by

`\begin{pmatrix}{8} \\ {m}\end{pmatrix}=(8!)/(m!(8-m)!),m=0,1,2,\ldots,8`

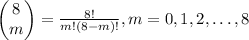
Plugging each m value on this equation, we have

`\begin{gathered} \begin{pmatrix}{8} \\ {0}\end{pmatrix}=(8!)/(0!(8-0)!)=(8!)/(8!)=1 \\ \begin{pmatrix}{8} \\ {1}\end{pmatrix}=(8!)/(1!(8-1)!)=(8!)/(7!)=8 \\ \begin{pmatrix}{8} \\ {2}\end{pmatrix}=(8!)/(2!(8-2)!)=(8\cdot7)/(2)=28 \\ \begin{pmatrix}{8} \\ {3}\end{pmatrix}=56 \\ \begin{pmatrix}{8} \\ {4}\end{pmatrix}=70 \\ \begin{pmatrix}{8} \\ {5}\end{pmatrix}=56 \\ \begin{pmatrix}{8} \\ {6}\end{pmatrix}=28 \\ \begin{pmatrix}{8} \\ {7}\end{pmatrix}=8 \\ \begin{pmatrix}{8} \\ {8}\end{pmatrix}=1 \end{gathered}`

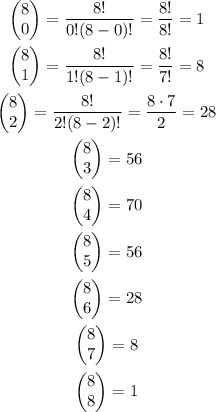
And those are the values on the eighth row.