Finding x
Step 1: "braking" fractions
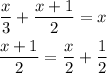
We replace the second in the original equation:
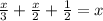
Step 2: rearraging the equation (the terms with x on one side, numbers on the other)
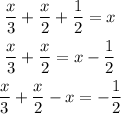
Step 3: adding fractions
Since
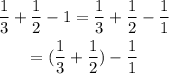
We know that
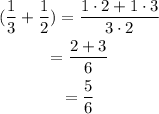
Replacing it:
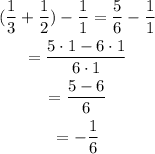
Then
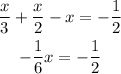
Step 4: finding x
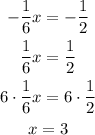
Answer: C.x=3