To find the area of the figure you can find the area of the figures that make it up and then add these areas, in other words
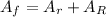
Where
The formula to find the area of a rectangle is
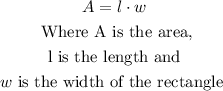
So, you have
![\begin{gathered} l_r=3\text{ mm} \\ w_r=1\text{ mm} \\ A_r=l_r\cdot w_r \\ A_r=3\operatorname{mm}\cdot1\operatorname{mm} \\ A_r=3\operatorname{mm}^2 \end{gathered}]()
![\begin{gathered} l_R=6\text{ mm} \\ w_R=2\text{ mm} \\ A_R=l_R\cdot w_R \\ A_R=6\operatorname{mm}\cdot2\operatorname{mm} \\ A_R=12\operatorname{mm}^2 \end{gathered}]()
Finally, adding the areas you have
![\begin{gathered} A_f=A_r+A_R \\ A_f=3\operatorname{mm}^2+12\operatorname{mm}^2 \\ A_f=15\operatorname{mm}^2 \end{gathered}]()
Therefore, the area of the figure is 15 square milimeters.