Question

This graph shows a proportional relationship.

What is the constant of proportionality?

Enter your answer as a decimal in the box.

Answer 1

The constant of proportionality is 0.3

Explanation:

» The graph shows a direct proportiinality.

`{ \rm{y \: \alpha \: x}}`

» Therefore, input the constant;

`{ \rm{y = kx}}`

» When x is 5, y is 1.5:

`{ \tt{1.5 = (k * 5)}} \\ { \rm{k = 0.3}}`

Answer 2

0.3

Explanation:

On a graph, proportional relationships are straight lines that extend through the origin.

Slope of a graph = constant of proportionality of the equation

Let (5, 1.5) =
`(x_1,y_1)`

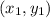
Let (20, 6) =
`(x_2,y_2)`

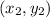
Formula of a slope:
`m=(y_2-y_1)/(x_2-x_1)`

`\implies m=(6-1.5)/(20-5)=0.3`

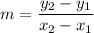
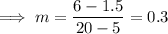
So as the slope = 0.3, the constant of proportionality = 0.3