First we get rid of the parenthesis on the right side by using the distributive property:
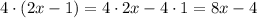
then, we would have the following equivalent expression:
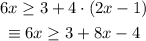
Now we solve for x. First we get all the terms with an 'x' to one side of the inequaility. In this case, we will pass the 8x to the other side with its sign changed:
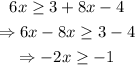
Since the -2 is multiplying the x, we have to pass it to the other side dividing the -1 but since it's negative, the inequality sign will change:

We have that x <= 1/2, then, the correct representation of the inequality is: