The quadratic equation given in the question is
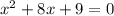
Step 1: Keep x terms on the left and move the constant to the right side by subtracting 9 on both sides
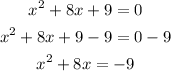
Step 2: Take half of the coefficient of the x term and square it
The coefficient of the x term is 8
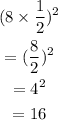
Step 3: Add 16 to both sides in the equation in step 1

Step 4: Re-write the perfect squares on the left
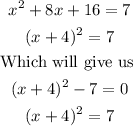
Hence,
We will have (x+4)²=7
To solve for the value of x, we will equate to zeros and make x the subject of the formula
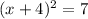
Step 5: Add 7 to both sides

Step 6: Square root both sides
![\begin{gathered} (x+4)^2=7 \\ \sqrt[]{(x+4)}^2=\sqrt[]{7} \\ (x+4)=\pm\sqrt[]{7} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/cc4ehtlalt5qbeavpjxtq88sm7g9ix4tms.png)
Step 7: Isolate the x on the left side and solve for x by subtracting 4 from both sides
![\begin{gathered} (x+4)=\pm\sqrt[]{7} \\ x+4-4=\pm\sqrt[]{7}-4 \\ x=\pm\sqrt[]{7}-4 \\ \text{therefore,} \\ x=-4+\sqrt[]{7} \\ x=-4-\sqrt[]{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k82eivnu5rxc5cu4x7du18664pyj02yx2s.png)
Therefore,
The value of x is
x = -4+√7 , -4-√7