Question

The following table shows the breakdown of opinions for both faculty and students in a recent survey about the new reconstructing of the campus to include an honors college. find the probability that a randomly selected person is either a faculty member in favor of the change or a student who has an opinion either for or against. express your answer as a fraction.

Answer 1

Given:

The objective is to find the probability that a randomly selected person is either a faculty member in favor of the change or a student who has an opinion either for or against.

Step-by-step explanation:

The required probability can be calculated as,

`P(\text{AorB)}=P(A)+P(B)-P(AandB)\text{ . . . .(1)}`

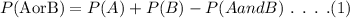
Here, P(A) represents the probability of faculty member in favor of the change, P(B) represents the probability of student who has an opinion either for or against.

The probability of faculty member in favor of the change can be calculated as, T

`P(A)=(7)/(217)\text{ . . . .(2)}`

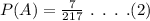
The probability of student who has an opinion either for or against can be calculated as,

`\begin{gathered} P(B)=(69)/(217)+(75)/(217) \\ P(B)=(144)/(217)\text{ . . . . . .(3)} \end{gathered}`

Since, it is mutually exclusive events,

`P(\text{AandB)}=0\text{ . . . . . . .(4)}`

To find P(A or B):

On plugging the equations (2), (3) and (4) in equation (1),

`\begin{gathered} P(\text{AorB)}=(7)/(217)+(144)/(217)+0 \\ =(151)/(217) \end{gathered}`

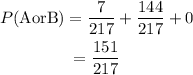
Hence, the probability that a randomly selected person is either a faculty member in favor of the change or a student who has an opinion either for or against is 151/217.