Question

Solve this system of equations byusing the elimination method.3x + 4y = 4-X – 3y = 7=\וז ו7ro

Answer 1

Given:

System of equation is given as

`\begin{gathered} 3x+4y=4 \\ -x-3y=7 \end{gathered}`

Required:

Solve system of equation by using the method elimination.

Step-by-step explanation:

By using the elimination method

we multiply second equation with 3 and then add in first equation

because by doing this process we eliminate the x

`\begin{gathered} 3x+4y+3(-x-3y)=4+3*7 \\ 3x+4y-3x-9y=4+21 \\ -5y=25 \\ y=-5 \end{gathered}`

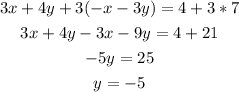
now put the value of y in first equation

`\begin{gathered} 3x+4(-5)=4 \\ 3x-20=4 \\ 3x=20+4 \\ 3x=24 \\ x=8 \end{gathered}`

Final answer:

Solution of given system of equation is (8,-5)