Let x be the number of adult tickets and let y be the number of children.
We know that in total there were sold 700 tickets, that means:
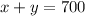
Now we know that each adult ticket was $2 and the children's tickets was $1, and that the total was $900, this means that:
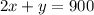
Then we have the following system of equations:
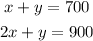
To solve it we substract the second equation from the first one, then we have:
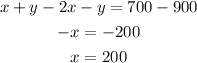
Now that we have the value of x we plug it in the first equation to find y:

Therefore, there were 200 adult's tickets and 500 children's tickets sold.