Question

Emily is standing 24 feet away from a light pole. The distance between Emily to a point of tangency on the pole is 12 feet. What is the radius of the light pole?Note : In the figure distance between Emily and the point of tangency is marked as 24 ft instead of 12.

Answer 1

From the given figure,

AB = Distance between Emily to a point of tangency.

BC = Radius of the pole

AC = Distance between Emily and the pole.

ABC is a right angled triangle at B.

Now,

`\begin{gathered} In\text{ }\Delta ABC\text{ , By Using Pythagoras theorem } \\ AC^2=AB^2+BC^2 \end{gathered}`

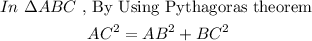
Substituting the given values in the statement,

`\begin{gathered} 24^2=12^2+r^2 \\ r^2=24^2-12^2 \\ r^2\text{ = }432 \\ r\text{ = 20.78 ft} \end{gathered}`

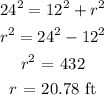
Thus the radius of the pole is 20.78 ft .