Question

Michael launched a new website to share news and photos of his town. The equation below estimates the number of followers, y, in x weeks after his launch. y = 82(1.045)^x Complete each of the 2 activities for this Task. Activity 1 of 2 What is the rate of growth for the number of followers each week? A 45% B. 1,045% C. 4.5% D. 82% Activity 2 of 2 How many followers should Michael expect in the 4th week? Round to the nearest whole number. Show your work please!

Answer 1

Consider the given expression,

`y=82(1.045)^x`

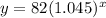
The first derivative gives the rate of growth for the number of followers.

Solve for the first derivative as,

`\begin{gathered} (dy)/(dx)=82*(d \square)/(dx)(1.045)^x \\ (dy)/(dx)=82*(1.045)^x\ln (1.045) \\ (dy)/(dx)=y*0.045 \\ (dy)/(dx)=4.5\text{ percent of y} \end{gathered}`

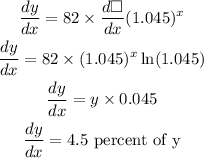
Thus, the rate of growth of followers is approximately 4.5% each week.

Therefore, option C is the correct choice.

The number of followers corresponding to the 4th week is calculated as,

`y=82*(1.045)^4=82*1.1925=97.7865\approx98`

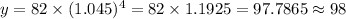
Thus, Michael should expect approximately 98 followers in 4th week.