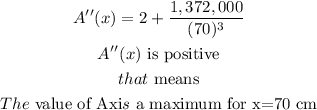step 1
Find out the equation of the volume of the box
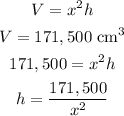
step 2
Find out the expression for the surface area
The surface area is given by the expression
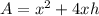
substitute the value of h
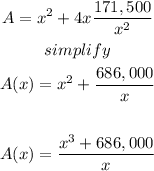
step 3
Find out the derivative A'(x)
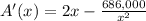
step 4
Equate the derivative to zero
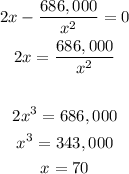
A'(x)=0 when x=70
step 5
Find out the second derivative A''(x)
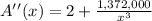
Evaluate the second derivative for x=70