Answer:
If the average rate of change in the data is negative, based on the variables analyzed;
b. It means that the median age of a man at the time of his first marriage is decreasing
Explanation:
The given data is presented as follows;
Year;
 1910, 1920, 1930, 1940, 1950, 960, 1970, 1980, 1990, 2000
1910, 1920, 1930, 1940, 1950, 960, 1970, 1980, 1990, 2000
Median Age;
 25.1, 24.6, 24.3, 24.3, 22.8, 22.8, 23.2, 24.7, 26.1, 26.8
25.1, 24.6, 24.3, 24.3, 22.8, 22.8, 23.2, 24.7, 26.1, 26.8
The date points are plotted on a graph using Microsoft Excel
 The corresponding change in years, Δx, is positive because, we have;
The corresponding change in years, Δx, is positive because, we have;
Δx = x₂ - x₁ = Higher year - Previous year
Therefore, for a negative average rate of change, we have;
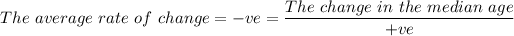
∴ The change in the median age, Δy = +ve × (-ve) = -ve (negative)
Δy = -ve
∴ Δy = Median age for higher year - Median age for previous year = -ve
Median age for higher year = -(y) + Median age for previous year
Where 'y' is positive
∴ Median age for subsequent year < Median age for previous year
Therefore, if the average rate of change is negative, the median age of a man's first marriage is decreasing