The domain of a function is the set of all x-values the function can take.
Since we have a radical symbol, (x² - 1) must not be equal to a negative number because it will make the function undefined.
For the function (x² - 1), the value of x must be greater than 1 or less than -1 in order for the function to be defined.

If for instance, the value of x is 0.5, the value of (x² - 1) will be -0.75 and the square root of a negative number is undefined. Therefore, we must not have an x-value that is less than 1 or greater than -1.
Hence, the domain of this function in interval notation is:
![(-\infty,-1]\cup[1,\infty)](https://img.qammunity.org/2023/formulas/mathematics/college/dzx9l96gtjul2a2zp33w6wim8i9glczzun.png)
In set notation, it is x.
In order to graph the function, let's assume some values of x that are found in the domain.
For the domain, x ≤ -1, we can assume x = -1, x = -2, and x = -3.
At x = -1, y = 1.
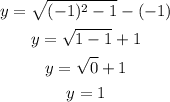
At x = -2, y = 3.73
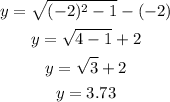
At x = -3, y = 5.83.
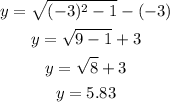
For the domain x ≥ 1, we can assume x = 1, x = 2, and x = 3.
At x = 1, y = -1.
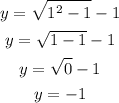
At x = 2, y = -0.268

At x = 3, y = -0.172.

Let's plot the 6 coordinates. The graph of this function, with limits indicated, is shown below.