Question

A football is kicked with a velocity of 32.0m/s and at an angle of 42 degrees it takes 4.40s. How high does it travel?

Answer 1

23.4 m

Step-by-step explanation

to solve this we need to use the expression:

`h=v\sin (\theta)t-(gt^2)/(2)`

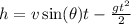
where

`\begin{gathered} h\text{ is the heigth} \\ v\text{ is initial velocity} \\ \theta\text{ is the angle} \\ t\text{ is the time} \end{gathered}`

then, let

`\begin{gathered} v=32\text{ m/s} \\ \theta=42\text{ \degree} \\ t=4.4\text{ s} \\ g=9.8\text{ }(m)/(s^2) \end{gathered}`

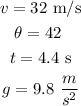
now, replace

`\begin{gathered} h=v\sin (\theta)t-(gt^2)/(2) \\ h=32\sin (42)(4.40)-((9.8)(4.4^2))/(2) \\ h=94.21-94.864 \\ h=-0.654 \end{gathered}`

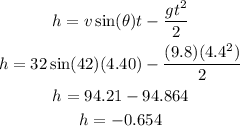
let's check the time of flight

`\begin{gathered} t=(2v\sin\theta)/(g) \\ t=(2\cdot32\cdot\sin(42))/(9.8) \\ t=4.36 \end{gathered}`

it means after 4.36 the ball is on the ground.

Step 2

so, to find the maximum heigth we need to use the expression

`\begin{gathered} y_(\max )=(v^2\sin ^2\theta)/(2g) \\ \text{replace} \\ y_(\max )=((32)^2\sin ^2(42))/(2(9.8)) \\ y_(\max )=(1024\cdot0.4477)/(2(9.8)) \\ y_(\max )=(458.48)/(19.6) \\ y_(\max )=23.39 \end{gathered}`

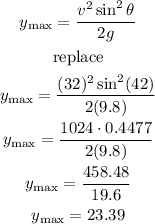
therefore, the answer is

23.4 m

I hope this helps you