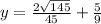To find the horizontal tangent line, we have to conduct the first derivative test. The first derivative test sets the derivative of the function equal to 0.
Let's start out with finding the derivative of the function:
It seems like we will have to use Quotient Rule.
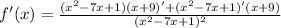
Now we can use basic derivative rules and properties to find the final derivative:
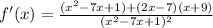
Setting the derivative equal to 0, we can begin the first derivative test:

We can simplify the derivative before solving (expand and combine like terms):
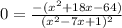
From here, we need to determine our values of x that will make the derivative equal to 0 or undefined. In this case, since we are not trying to find relative maxima or minima, we just need to find where the entire derivative is equal to 0. We can simply just graph the numerator and find its roots:
We can see that the values of x will be -21.0416 and 3.04159 will be the values that make the derivative equal to 0.
Also recall what the derivative is. The derivative is the slope of the tangent line. In order to find the horizontal tangent line, we know that horizontal tangent lines' slope is equal to 0.
Therefore, we can use either value of x to now find our equation.
Recall what the point-slope form of a line is:

Since we know that the derivative slope must equal 0, then we know that m = 0. We now need to find a point (x, y). Substitute one of the x values into the original equation to find an actual point on the function (remember not to round intermediate values on your calculator!):
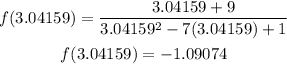
Now we have a point (x, y) (I will put it in the actual radical form here):

Substitute our variables into point-slope form:
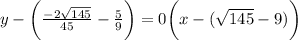
Simplify and rewrite to obtain our final answer: