Answer:
0.3
Explanation:
On a graph, proportional relationships are straight lines that extend through the origin.
Slope of a graph = constant of proportionality of the equation
Let (5, 1.5) =
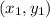
Let (20, 6) =
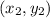
Formula of a slope:

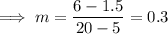
So as the slope = 0.3, the constant of proportionality = 0.3