In order to find what factors could represent the length and the width, we need to factor the polynomial that represents the area.
To do so, first let's find the zeros a1 and a2, then we can factor as follows:
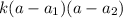
Where k is the coefficient of the quadratic term (so k = 12).
Using the quadratic formula, we have:
![\begin{gathered} 12a^2+4a-5=0 \\ a_{}=\frac{-4+\sqrt[]{4^2-4\cdot12\cdot(-5)}}{2\cdot12} \\ a_1=(-4+16)/(24)=(1)/(2) \\ a_2=(-4-16)/(24)=-(5)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5ijhbzred859zasivy65ea5asesmckqhtz.png)
Then, we have:
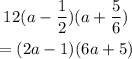
Therefore the factors are 2a-1 and 6a+5.