Question

Evaluate ∫(15x2+x2‾‾√34) dx. Here C is the constant of integration.

Answer 1

We use the following formula for integration:

`\int x^ndx=(x^(n+1))/(n+1)+C`

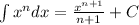
We have the following integral:

`\int(15x^2+\frac{\sqrt[3]{x^2}}{4})dx`

Separate into two integrals:

`\int(15x^2+\frac{\sqrt[3]{x^2}}{4})dx=\int15x^2dx+\int\frac{\sqrt[3]{x^2}}{4}dx`

Calculate the first integral. Take the coefficient out of the integral:

`\int15x^2dx=15\int x^2dx`

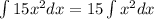
Apply the integration formula:

`\int15x^2dx=15(x^3)/(3)+C=5x^3+C`

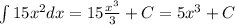
Calculate the second integral. Take the coefficient out of the integral:

`\int\frac{\sqrt[3]{x^2}}{4}dx=(1)/(4)\int\sqrt[3]{x^2}dx`

Express the radical as a fractional exponent:

`(1)/(4)\int\sqrt[3]{x^2}dx=(1)/(4)\int x^(2/3)dx`

Apply the integration formula:

`(1)/(4)\cdot(x^(5/3))/(5/3)+C=(3)/(20)\sqrt[3]{x^5}+C`

The total integral is:

`\int(15x^2+\frac{\sqrt[3]{x^2}}{4})dx=5x^3+(3)/(20)\sqrt[3]{x^5}+C`