SOLUTION
(a) From the information given in the question,
We will select a curve with 58 at its center which represents the mean and
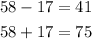
41 and 75 at the left and right sides. That is gotten by subtracting and adding the standard deviation of 17.
Hence the answer is Graph D
(b) The region that represents less than 41 is seen in graph B
Hence graph B is the answer
(c) Option A
The probability is 0.1587 that a randomly selected cell phone plan in this population is less than $41 per month