Question

In an internet video an athlete launches a basketball from a stadium platform that is 16.2m higher than the hoop. He makes the basket by launching the ball at an angle of 14.5 degrees above the horizontal with a speed of 11.6 m/s. What horizontal distance does the ball travel before passing through the hoop?

Answer 1

First, lets draw a diagram of the situation

From what we are given, we know couple of things

First:

We know that the net vertical distance travelled is 16.2 meters down

inital velocity is 16.2 meters

And that the acceleration of the ball downwards is 9.8 m/s^2

Lets start by working backwards and figuring out what we need

Using kinematics, we know that the formula we need to find the horizontal distance is

`\Delta x=v_xt`

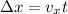
where x is the distance traveled, vx is the horizontal speed and t is time

We can figure vx right now by finding the horizontal component of speed.

`v_x=v_0cos(14.5)`

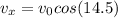
which yields us vx = 11.23 m/s

Now we have to find time traveled.

For this, we will need to use the vertical components

Since we have acceleration, inital speed, and distance traveled and we are finding time, we can use the formula

`\Delta y=v_yt+(1)/(2)at^2`

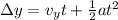
To find vy, we just use the same formula we used for vx except we use sin instead of cos. This yields us 2.9 m/s for initial vertical speed.

Plugging in our values, we have

-16.2 = (2.9)t + 1/2(-9.8)(t^2)

To solve for t, we can use the quadratic formula

1/2(-9.8)t^2 + 2.9t + 16.2 = 0

-4.9t^2 + 2.9t + 16.2 = 0

The quadratic formula is as shown

`t=(-b\pm√(b^2-4ac))/(2a)`

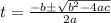
Where t is what we solve for, a is the coefficient for the first term (the t^2), b is the coefficient for the second term (t), and c is the coefficient for the last term (16.2).

Plugging these values in (a = -4.9, b = 2.9, c = 16.2) gets us t

`t=(-2.9\pm√((2.9)^2-4(-4.9)(16.2)))/(2(-4.9))`
`t=(2.9\pm√(8.41+317.52))/(9.8)`
`t=(2.9\pm18.054)/(9.8)`
`t=(20.95)/(9.8),t=(-15.15)/(9.8)`
`t=\lbrace2.14\rbrace-1.55`

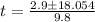
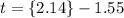
We solve for t, which gets us 2.14 seconds (we don't use the negative value since we start at t = 0 and time moves forward).

now that we know both time and horizontal speed, we can multiply both of them together to get horizontal distance.

`\Delta x=v_xt`
`\Delta x=11.23(2.14)`

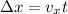
This equals 24.012 meters traveled