ANSWER:
39.2 m/s^2
Explanation:
We have to acceleration due to gravity at the surface of planet:
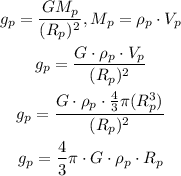
Where,
Mp = mass of planet
ρp = density of planet
Rp = radius of planet
Given:
ρp = 2ρe, Rp = 2Re
where,
ρe = density of earth
Re = radius of earth
Replacing:
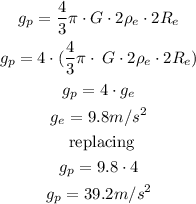
Therefore the acceleration due to gravity on the planet is 39.2 m/s^2