Question

A person places $84800 in an investment account earning an annual rate of 4.1%,compounded continuously. Using the formula V = Pert, where V is the value of theaccount in t years, P is the principal initially invested, e is the base of a naturallogarithm, and r is the rate of interest, determine the amount of money, to thenearest cent, in the account after 4 years.

Answer 1

$99,911.36

Step-by-step explanation:

Principal = P = $84800

rate = r = 4.1% = 0.041

t = 4 years

`\begin{gathered} \text{The given formula: } \\ V\text{ = P}e^(rt) \end{gathered}`
`\begin{gathered} V\text{ = 84800}e^(0.041*4) \\ V\text{ = 84800}e^(0.164) \\ V\text{ = 84800(1.1782}) \end{gathered}`
`V\text{ = }99911.36`

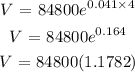
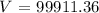
To the nearest cent is the same as to the nearest hndredth: V = $99911.36

The amount of money, to the nearest cent, in the account after 4 years iis $99,911.36