ANSWER
The future value of the investment is $2704.3515
Explanation:
Given information
The present value = $2700
Annual simple interest rate = 2.25%
number of compounded period = 8 months
Let the future value be F.V
To find the future value, we need to apply the below formula

Where
• FV = future value
,
• PV = Present value
,
• r = interest rate
,
• n = compounding period
The next thing is to convert 8 months to a year
let x be the number of years
Recall that,
12 months is equivalent to 1 year
8 months is equivalent to x years
Mathematically,
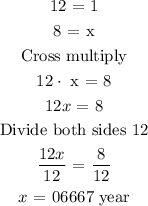
Using the above formula, we can now find the future value of the investment
