Question

The box contains red, white, and blue balls. The probability of pulling a red ball out of the box is 1/4,White - 3/20. Calculate the probability that one ball accidentally pulled out is:(a) blue; (b) red or white; (c) red or blue; (d) not white.

Answer 1

We have to find the listed probabilities.

We have red, white and blue balls.

Red balls have a probability of 1/4.

White balls have a probability of 3/20.

The complement of these probabiities correspond to blue balls.

a) We then can calculate the probability of a blue ball by calculating 1 minus the probability of not being a blue ball, which means red or white.

We can do it as:

`\begin{gathered} P(B)=1-P(not\text{ }B) \\ P(B)=1-(P(R)+P(W)) \\ P(B)=1-((1)/(4)+(3)/(20)) \\ P(B)=1-(5+3)/(20) \\ P(B)=1-(8)/(20) \\ P(B)=(20-8)/(20) \\ P(B)=(12)/(20) \\ P(B)=(3)/(5) \end{gathered}`

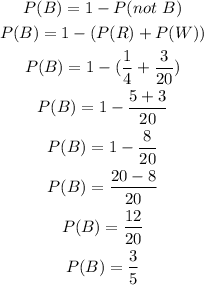
b) We now have to calculate the probability of the ball being red or white.

As it can be either of the two we can add the probabilities:

`\begin{gathered} P(R\cup W)=P(R)+P(W) \\ P(R\cup W)=(1)/(4)+(3)/(20) \\ P(R\cup W)=(8)/(20) \\ P(R\cup W)=(2)/(5) \end{gathered}`

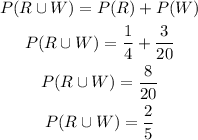
NOTE: It could have also being calculated as the complement of the probability of the ball being blue.

c) We now calculate the probability that the ball is red or blue. We will calculate it as the complement of the ball being white:

`\begin{gathered} P(R\cup B)=1-P(W) \\ P(R\cup B)=1-(3)/(20) \\ P(R\cup B)=(20)/(20)-(3)/(20) \\ P(R\cup B)=(17)/(20) \end{gathered}`

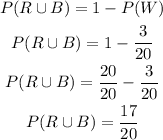
d) In this case, we will got the same result as in (c), as the event of the ball being red or blue its the same event as the ball being not white. So the probability is:

`P(not\text{ W})=P(R\cup B)=(17)/(20)`

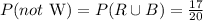
Answer:

a) 3/5

b) 2/5

c) 17/20

d) 17/20