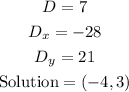Question

How to find the denominator, the associates of x & y

Answer 1

Given the following System of equations:

`\begin{cases}-3x+2y=18 \\ -2x-y=5\end{cases}`

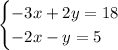
You can identify that it has this form:

`\begin{cases}a_1x+b_1y=c_1_{} \\ a_2x+b_2y=c_2\end{cases}`

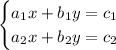
Where:

`\begin{gathered} a_1=-3 \\ a_2=-2 \\ b_1=2 \\ b_2=-1 \\ c_1=18_{} \\ c_2=5 \end{gathered}`

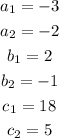
The determinant D is, by definition:

`D=\begin{bmatrix}{a_1} & {b_1} & {} \\ {a_2} & {b_2} & {} \\ {} & {} & \end{bmatrix}=a_1b_2-a_2b_1`

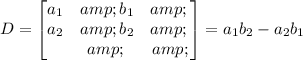
Then, in this case this is:

`D=\begin{bmatrix}{-3} & {2_{}} & {} \\ {-2_{}} & {-1_{}} & {} \\ {} & {} & \end{bmatrix}=(-3)(-1)-(-2)(2)=7`

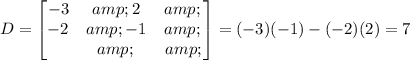
By definition, the determinant associated with "x" is given by:

`D_x=\begin{bmatrix}{c_1} & {b_1} & {} \\ {c_2} & {b_2} & {} \\ {} & {} & \end{bmatrix}=c_1b_2-c_2b_1`

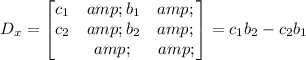
Then, in this case:

`D_x=\begin{bmatrix}{18_{}} & {2_{}} & {} \\ {5_{}} & {-1_{}} & {} \\ {} & {} & \end{bmatrix}=(18)(-1)-(5)(2)=-28`

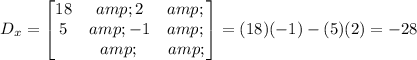
The determinant associated with "y" is given by:

`D_y=\begin{bmatrix}{a_1} & {c_1} & {} \\ {a_2} & {c_2} & {} \\ {} & {} & \end{bmatrix}=a_1c_2-a_2c_1`

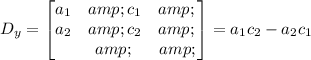
Then, this is:

`D_y=\begin{bmatrix}{-3_{}} & {18_{}} & {} \\ {-2_{}} & {5_{}} & {} \\ {} & {} & \end{bmatrix}=(-3)(5)-(-2)(18)=21`

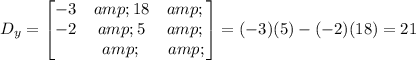
The solution of the System of equations can be found as following:

1. For the x-coordinate:

`x_{}=(D_x)/(D)=(-28)/(7)=-4`

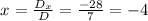
2. For the y-coordinate:

`y=(D_y)/(D)=(21)/(7)=3`

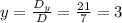
The answers are:

`\begin{gathered} D=7 \\ D_x=-28 \\ D_y=21 \\ \text{Solution}=(-4,3) \end{gathered}`