Question

If -xy-x=y+3 then find the equations of all tangent lines to the curve when y=1

Answer 1

1) Let's firstly plug into the equation, the quantity of y=1

`\begin{gathered} -xy-x=y+3 \\ -x-x=1+3 \\ -2x=4 \\ (-2x)/(-2)=(4)/(-2) \\ x=-2 \\ (-2,1) \end{gathered}`

Note that after we plugged into that we have a point (-2,1).

2) Now, let's take the first derivative from the original equation. In this case, we need to take an implicit differentiation as you can see it below:

`\begin{gathered} (d)/(dx)\lbrack-xy-x\rbrack=(d)/(dx)\lbrack y+3\rbrack \\ -(d)/(dx)\lbrack xy\rbrack-(d)/(dx)\lbrack x\rbrack=(d)/(dx)\lbrack y\rbrack+(d)/(dx)\lbrack3\rbrack \\ -xy^(\prime)-y-1=y^(\prime) \\ y^(\prime)=-(y+1)/(x+1) \end{gathered}`

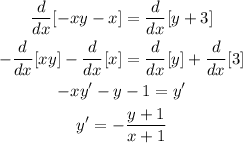
3) Let's now find the slope: