Answer:
• Slope= -3/4
,
• y-intercept = 4.5
Step-by-step explanation:
First, we express the line in the slop-intercept form:
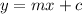
Given the line: 3x + 4y = 18
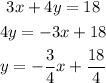
Therefore:
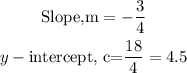
To graph the line, we use the x and y-intercepts.
When x=0, y=4.5 (0,4.5)
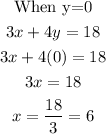
Therefore, when y=0, x=6 (6,0)
The line is attached below: